9  Survival Analysis

This chapter will provide hands-on instruction and exercises covering survival analysis using R. Some of the data to be used here will come from The Cancer Genome Atlas (TCGA), where we may also cover programmatic access to TCGA through Bioconductor if time allows.

Handouts: Download and print out these handouts and bring them to class:

9.1 Background

In the chapter on essential statistics (Chapter 8) we covered basic categorical data analysis – comparing proportions (risks, rates, etc) between different groups using a chi-square or fisher exact test, or logistic regression. For example, we looked at how the diabetes rate differed between males and females. In this kind of analysis you implicitly assume that the rates are constant over the period of the study, or as defined by the different groups you defined.

But, in longitudinal studies where you track samples or subjects from one time point (e.g., entry into a study, diagnosis, start of a treatment) until you observe some outcome event (e.g., death, onset of disease, relapse), it doesn’t make sense to assume the rates are constant. For example: the risk of death after heart surgery is highest immediately post-op, decreases as the patient recovers, then rises slowly again as the patient ages. Or, recurrence rate of different cancers varies highly over time, and depends on tumor genetics, treatment, and other environmental factors.

9.1.1 Definitions

Survival analysis lets you analyze the rates of occurrence of events over time, without assuming the rates are constant. Generally, survival analysis lets you model the time until an event occurs,1 or compare the time-to-event between different groups, or how time-to-event correlates with quantitative variables.

The hazard is the instantaneous event (death) rate at a particular time point t. Survival analysis doesn’t assume the hazard is constant over time. The cumulative hazard is the total hazard experienced up to time t.

The survival function, is the probability an individual survives (or, the probability that the event of interest does not occur) up to and including time t. It’s the probability that the event (e.g., death) hasn’t occured yet. It looks like this, where \(T\) is the time of death, and \(Pr(T>t)\) is the probability that the time of death is greater than some time \(t\). \(S\) is a probability, so \(0 \leq S(t) \leq 1\), since survival times are always positive (\(T \geq 0\)).

\[ S(t) = Pr(T>t) \]

The Kaplan-Meier curve illustrates the survival function. It’s a step function illustrating the cumulative survival probability over time. The curve is horizontal over periods where no event occurs, then drops vertically corresponding to a change in the survival function at each time an event occurs.

Censoring is a type of missing data problem unique to survival analysis. This happens when you track the sample/subject through the end of the study and the event never occurs. This could also happen due to the sample/subject dropping out of the study for reasons other than death, or some other loss to followup. The sample is censored in that you only know that the individual survived up to the loss to followup, but you don’t know anything about survival after that.2

Proportional hazards assumption: The main goal of survival analysis is to compare the survival functions in different groups, e.g., leukemia patients as compared to cancer-free controls. If you followed both groups until everyone died, both survival curves would end at 0%, but one group might have survived on average a lot longer than the other group. Survival analysis does this by comparing the hazard at different times over the observation period. Survival analysis doesn’t assume that the hazard is constant, but does assume that the ratio of hazards between groups is constant over time.3 This class does not cover methods to deal with non-proportional hazards, or interactions of covariates with the time to event.

Proportional hazards regression a.k.a. Cox regression is the most common approach to assess the effect of different variables on survival.

9.1.2 Cox PH Model

Kaplan-Meier curves are good for visualizing differences in survival between two categorical groups,4 but they don’t work well for assessing the effect of quantitative variables like age, gene expression, leukocyte count, etc. Cox PH regression can assess the effect of both categorical and continuous variables, and can model the effect of multiple variables at once.5

Cox PH regression models the natural log of the hazard at time t, denoted \(h(t)\), as a function of the baseline hazard (\(h_0(t)\)) (the hazard for an individual where all exposure variables are 0) and multiple exposure variables \(x_1\), \(x_1\), \(...\), \(x_p\). The form of the Cox PH model is:

\[ log(h(t)) = log(h_0(t)) + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p \]

If you exponentiate both sides of the equation, and limit the right hand side to just a single categorical exposure variable (\(x_1\)) with two groups (\(x_1=1\) for exposed and \(x_1=0\) for unexposed), the equation becomes:

\[ h_1(t) = h_0(t) \times e^{\beta_1 x_1} \]

Rearranging that equation lets you estimate the hazard ratio, comparing the exposed to the unexposed individuals at time t:

\[ HR(t) = \frac{h_1(t)}{h_0(t)} = e^{\beta_1} \]

This model shows that the hazard ratio is \(e^{\beta_1}\), and remains constant over time t (hence the name proportional hazards regression). The \(\beta\) values are the regression coefficients that are estimated from the model, and represent the \(log(Hazard\, Ratio)\) for each unit increase in the corresponding predictor variable. The interpretation of the hazards ratio depends on the measurement scale of the predictor variable, but in simple terms, a positive coefficient indicates worse survival and a negative coefficient indicates better survival for the variable in question.

9.2 Survival analysis in R

The core survival analysis functions are in the survival package. The survival package is one of the few “core” packages that comes bundled with your basic R installation, so you probably didn’t need to install.packages() it. But, you’ll need to load it like any other library when you want to use it. We’ll also be using the dplyr package, so let’s load that too. Finally, we’ll also want to load the survminer package, which provides much nicer Kaplan-Meier plots out-of-the-box than what you get out of base graphics.

The core functions we’ll use out of the survival package include:

  • Surv(): Creates a survival object.
  • survfit(): Fits a survival curve using either a formula, of from a previously fitted Cox model.
  • coxph(): Fits a Cox proportional hazards regression model.

Other optional functions you might use include:

  • cox.zph(): Tests the proportional hazards assumption of a Cox regression model.
  • survdiff(): Tests for differences in survival between two groups using a log-rank / Mantel-Haenszel test.6

Surv() creates the response variable, and typical usage takes the time to event,7 and whether or not the event occured (i.e., death vs censored). survfit() creates a survival curve that you could then display or plot. coxph() implements the regression analysis, and models specified the same way as in regular linear models, but using the coxph() function.

9.2.1 Getting started

We’re going to be using the built-in lung cancer dataset8 that ships with the survival package. You can get some more information about the dataset by running ?lung. The help tells us there are 10 variables in this data:

  1. inst: Institution code
  2. time: Survival time in days
  3. status: censoring status 1=censored, 2=dead
  4. age: Age in years
  5. sex: Male=1 Female=2
  6. ph.ecog: ECOG performance score (0=good 5=dead)
  7. ph.karno: Karnofsky performance score as rated by physician
  8. pat.karno: Karnofsky performance score as rated by patient
  9. meal.cal: Calories consumed at meals
  10. wt.loss: Weight loss in last six months

You can access the data just by running lung, as if you had read in a dataset and called it lung. You can operate on it just like any other data frame.

head(lung)
class(lung)
dim(lung)
View(lung)

Notice that lung is a plain data.frame object. You could see what it looks like as a tibble (prints nicely, tells you the type of variable each column is). You could then reassign lung to the as_tibble()-ified version.

as_tibble(lung)
lung <- as_tibble(lung)
lung

9.2.2 Survival Curves

Check out the help for ?Surv. This is the main function we’ll use to create the survival object. You can play fast and loose with how you specify the arguments to Surv. The help tells you that when there are two unnamed arguments, they will match time and event in that order. This is the common shorthand you’ll often see for right-censored data. The alternative lets you specify interval data, where you give it the start and end times (time and time2). If you keep reading you’ll see how Surv tries to guess how you’re coding the status variable. It will try to guess whether you’re using 0/1 or 1/2 to represent censored vs “dead”, respectively.9

Try creating a survival object called s, then display it. If you go back and head(lung) the data, you can see how these are related. It’s a special type of vector that tells you both how long the subject was tracked for, and whether or not the event occured or the sample was censored (shown by the +).

s <- Surv(lung$time, lung$status)
class(s)
[1] "Surv"
s
  [1]  306   455  1010+  210   883  1022+  310   361   218   166   170   654 
 [13]  728    71   567   144   613   707    61    88   301    81   624   371 
 [25]  394   520   574   118   390    12   473    26   533   107    53   122 
 [37]  814   965+   93   731   460   153   433   145   583    95   303   519 
 [49]  643   765   735   189    53   246   689    65     5   132   687   345 
 [61]  444   223   175    60   163    65   208   821+  428   230   840+  305 
 [73]   11   132   226   426   705   363    11   176   791    95   196+  167 
 [85]  806+  284   641   147   740+  163   655   239    88   245   588+   30 
 [97]  179   310   477   166   559+  450   364   107   177   156   529+   11 
[109]  429   351    15   181   283   201   524    13   212   524   288   363 
[121]  442   199   550    54   558   207    92    60   551+  543+  293   202 
[133]  353   511+  267   511+  371   387   457   337   201   404+  222    62 
[145]  458+  356+  353   163    31   340   229   444+  315+  182   156   329 
[157]  364+  291   179   376+  384+  268   292+  142   413+  266+  194   320 
[169]  181   285   301+  348   197   382+  303+  296+  180   186   145   269+
[181]  300+  284+  350   272+  292+  332+  285   259+  110   286   270    81 
[193]  131   225+  269   225+  243+  279+  276+  135 
 [ reached getOption("max.print") -- omitted 28 entries ]
head(lung)
# A tibble: 6 × 10
   inst  time status   age   sex ph.ecog ph.karno pat.karno meal.cal wt.loss
  <dbl> <dbl>  <dbl> <dbl> <dbl>   <dbl>    <dbl>     <dbl>    <dbl>   <dbl>
1     3   306      2    74     1       1       90       100     1175      NA
2     3   455      2    68     1       0       90        90     1225      15
3     3  1010      1    56     1       0       90        90       NA      15
4     5   210      2    57     1       1       90        60     1150      11
5     1   883      2    60     1       0      100        90       NA       0
6    12  1022      1    74     1       1       50        80      513       0

Now, let’s fit a survival curve with the survfit() function. See the help for ?survfit. Here we’ll create a simple survival curve that doesn’t consider any different groupings, so we’ll specify just an intercept (e.g., ~1) in the formula that survfit expects. We can do what we just did by “modeling” the survival object s we just created against an intercept only, but from here out, we’ll just do this in one step by nesting the Surv() call within the survfit() call, and similar to how we specify data for linear models with lm(), we’ll use the data= argument to specify which data we’re using. Similarly, we can assign that to another object called sfit (or whatever we wanted to call it).

survfit(s~1)
Call: survfit(formula = s ~ 1)

       n events median 0.95LCL 0.95UCL
[1,] 228    165    310     285     363
survfit(Surv(time, status)~1, data=lung)
Call: survfit(formula = Surv(time, status) ~ 1, data = lung)

       n events median 0.95LCL 0.95UCL
[1,] 228    165    310     285     363
sfit <- survfit(Surv(time, status)~1, data=lung)
sfit
Call: survfit(formula = Surv(time, status) ~ 1, data = lung)

       n events median 0.95LCL 0.95UCL
[1,] 228    165    310     285     363

Now, that object itself isn’t very interesting. It’s more interesting to run summary on what it creates. This will show a life table.

summary(sfit)
Call: survfit(formula = Surv(time, status) ~ 1, data = lung)

 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    5    228       1   0.9956 0.00438       0.9871        1.000
   11    227       3   0.9825 0.00869       0.9656        1.000
   12    224       1   0.9781 0.00970       0.9592        0.997
   13    223       2   0.9693 0.01142       0.9472        0.992
   15    221       1   0.9649 0.01219       0.9413        0.989
   26    220       1   0.9605 0.01290       0.9356        0.986
   30    219       1   0.9561 0.01356       0.9299        0.983
   31    218       1   0.9518 0.01419       0.9243        0.980
   53    217       2   0.9430 0.01536       0.9134        0.974
   54    215       1   0.9386 0.01590       0.9079        0.970
   59    214       1   0.9342 0.01642       0.9026        0.967
   60    213       2   0.9254 0.01740       0.8920        0.960
   61    211       1   0.9211 0.01786       0.8867        0.957
   62    210       1   0.9167 0.01830       0.8815        0.953
   65    209       2   0.9079 0.01915       0.8711        0.946
   71    207       1   0.9035 0.01955       0.8660        0.943
   79    206       1   0.8991 0.01995       0.8609        0.939
   81    205       2   0.8904 0.02069       0.8507        0.932
   88    203       2   0.8816 0.02140       0.8406        0.925
   92    201       1   0.8772 0.02174       0.8356        0.921
   93    199       1   0.8728 0.02207       0.8306        0.917
   95    198       2   0.8640 0.02271       0.8206        0.910
  105    196       1   0.8596 0.02302       0.8156        0.906
  107    194       2   0.8507 0.02362       0.8056        0.898
  110    192       1   0.8463 0.02391       0.8007        0.894
  116    191       1   0.8418 0.02419       0.7957        0.891
  118    190       1   0.8374 0.02446       0.7908        0.887
  122    189       1   0.8330 0.02473       0.7859        0.883
 [ reached getOption("max.print") -- omitted 111 rows ]

These tables show a row for each time point where either the event occured or a sample was censored. It shows the number at risk (number still remaining), and the cumulative survival at that instant.

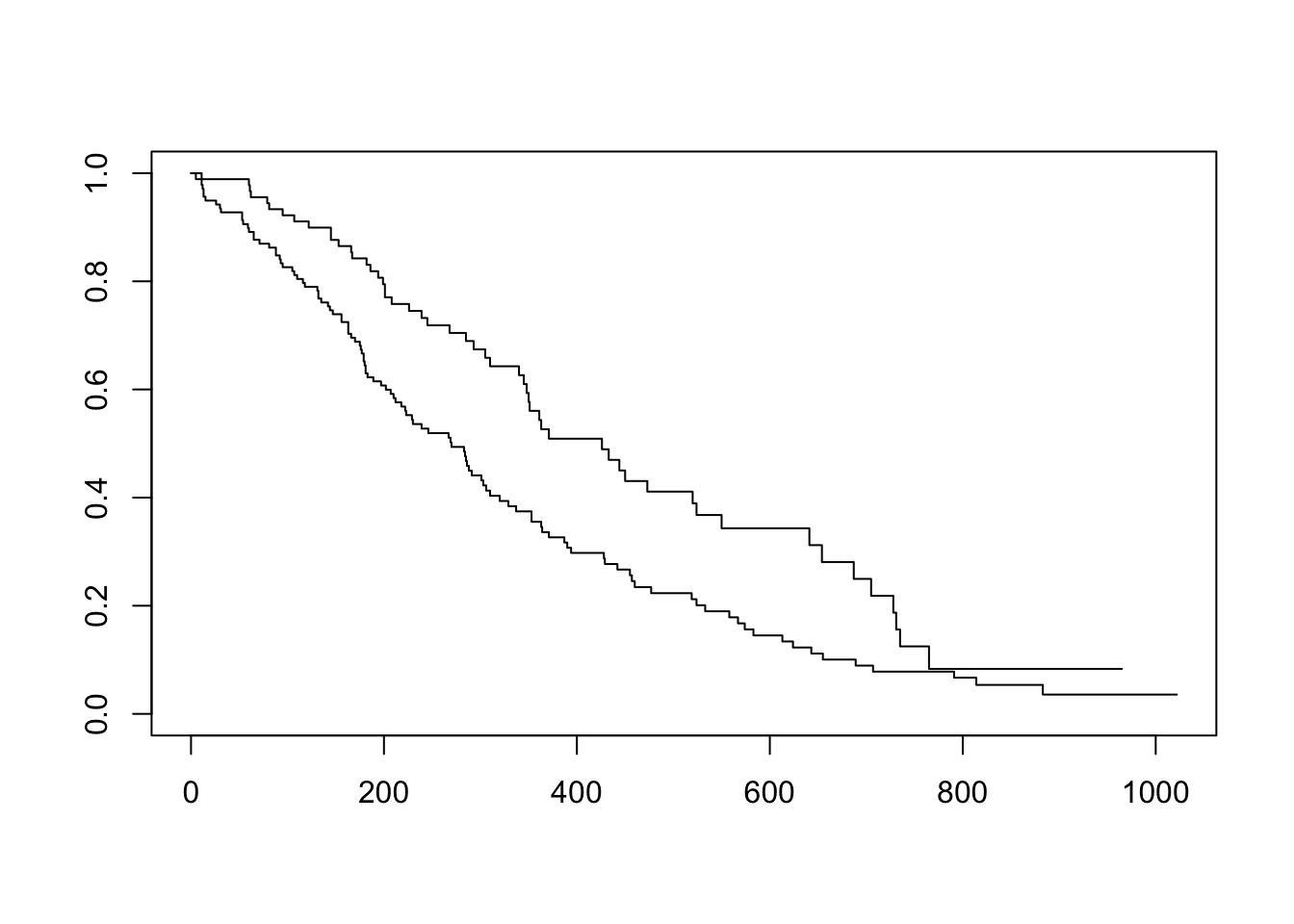
What’s more interesting though is if we model something besides just an intercept. Let’s fit survival curves separately by sex.

sfit <- survfit(Surv(time, status)~sex, data=lung)
sfit
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)

        n events median 0.95LCL 0.95UCL
sex=1 138    112    270     212     310
sex=2  90     53    426     348     550
summary(sfit)
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)

                sex=1 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
   11    138       3   0.9783  0.0124       0.9542        1.000
   12    135       1   0.9710  0.0143       0.9434        0.999
   13    134       2   0.9565  0.0174       0.9231        0.991
   15    132       1   0.9493  0.0187       0.9134        0.987
   26    131       1   0.9420  0.0199       0.9038        0.982
   30    130       1   0.9348  0.0210       0.8945        0.977
   31    129       1   0.9275  0.0221       0.8853        0.972
   53    128       2   0.9130  0.0240       0.8672        0.961
   54    126       1   0.9058  0.0249       0.8583        0.956
   59    125       1   0.8986  0.0257       0.8496        0.950
   60    124       1   0.8913  0.0265       0.8409        0.945
   65    123       2   0.8768  0.0280       0.8237        0.933
   71    121       1   0.8696  0.0287       0.8152        0.928
   81    120       1   0.8623  0.0293       0.8067        0.922
   88    119       2   0.8478  0.0306       0.7900        0.910
   92    117       1   0.8406  0.0312       0.7817        0.904
   93    116       1   0.8333  0.0317       0.7734        0.898
   95    115       1   0.8261  0.0323       0.7652        0.892
  105    114       1   0.8188  0.0328       0.7570        0.886
  107    113       1   0.8116  0.0333       0.7489        0.880
  110    112       1   0.8043  0.0338       0.7408        0.873
  116    111       1   0.7971  0.0342       0.7328        0.867
  118    110       1   0.7899  0.0347       0.7247        0.861
  131    109       1   0.7826  0.0351       0.7167        0.855
  132    108       2   0.7681  0.0359       0.7008        0.842
  135    106       1   0.7609  0.0363       0.6929        0.835
  142    105       1   0.7536  0.0367       0.6851        0.829
  144    104       1   0.7464  0.0370       0.6772        0.823
 [ reached getOption("max.print") -- omitted 71 rows ]

                sex=2 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    5     90       1   0.9889  0.0110       0.9675        1.000
   60     89       1   0.9778  0.0155       0.9478        1.000
   61     88       1   0.9667  0.0189       0.9303        1.000
   62     87       1   0.9556  0.0217       0.9139        0.999
   79     86       1   0.9444  0.0241       0.8983        0.993
   81     85       1   0.9333  0.0263       0.8832        0.986
   95     83       1   0.9221  0.0283       0.8683        0.979
  107     81       1   0.9107  0.0301       0.8535        0.972
  122     80       1   0.8993  0.0318       0.8390        0.964
  145     79       2   0.8766  0.0349       0.8108        0.948
  153     77       1   0.8652  0.0362       0.7970        0.939
  166     76       1   0.8538  0.0375       0.7834        0.931
  167     75       1   0.8424  0.0387       0.7699        0.922
  182     71       1   0.8305  0.0399       0.7559        0.913
  186     70       1   0.8187  0.0411       0.7420        0.903
  194     68       1   0.8066  0.0422       0.7280        0.894
  199     67       1   0.7946  0.0432       0.7142        0.884
  201     66       2   0.7705  0.0452       0.6869        0.864
  208     62       1   0.7581  0.0461       0.6729        0.854
  226     59       1   0.7452  0.0471       0.6584        0.843
  239     57       1   0.7322  0.0480       0.6438        0.833
  245     54       1   0.7186  0.0490       0.6287        0.821
  268     51       1   0.7045  0.0501       0.6129        0.810
  285     47       1   0.6895  0.0512       0.5962        0.798
  293     45       1   0.6742  0.0523       0.5791        0.785
  305     43       1   0.6585  0.0534       0.5618        0.772
  310     42       1   0.6428  0.0544       0.5447        0.759
  340     39       1   0.6264  0.0554       0.5267        0.745
 [ reached getOption("max.print") -- omitted 23 rows ]

Now, check out the help for ?summary.survfit. You can give the summary() function an option for what times you want to show in the results. Look at the range of followup times in the lung dataset with range(). You can create a sequence of numbers going from one number to another number by increments of yet another number with the seq() function.

# ?summary.survfit
range(lung$time)
[1]    5 1022
seq(0, 1100, 100)
 [1]    0  100  200  300  400  500  600  700  800  900 1000 1100

And we can use that sequence vector with a summary call on sfit to get life tables at those intervals separately for both males (1) and females (2). From these tables we can start to see that males tend to have worse survival than females.

summary(sfit, times=seq(0, 1000, 100))
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)

                sex=1 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    138       0   1.0000  0.0000       1.0000        1.000
  100    114      24   0.8261  0.0323       0.7652        0.892
  200     78      30   0.6073  0.0417       0.5309        0.695
  300     49      20   0.4411  0.0439       0.3629        0.536
  400     31      15   0.2977  0.0425       0.2250        0.394
  500     20       7   0.2232  0.0402       0.1569        0.318
  600     13       7   0.1451  0.0353       0.0900        0.234
  700      8       5   0.0893  0.0293       0.0470        0.170
  800      6       2   0.0670  0.0259       0.0314        0.143
  900      2       2   0.0357  0.0216       0.0109        0.117
 1000      2       0   0.0357  0.0216       0.0109        0.117

                sex=2 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0     90       0   1.0000  0.0000       1.0000        1.000
  100     82       7   0.9221  0.0283       0.8683        0.979
  200     66      11   0.7946  0.0432       0.7142        0.884
  300     43       9   0.6742  0.0523       0.5791        0.785
  400     26      10   0.5089  0.0603       0.4035        0.642
  500     21       5   0.4110  0.0626       0.3050        0.554
  600     11       3   0.3433  0.0634       0.2390        0.493
  700      8       3   0.2496  0.0652       0.1496        0.417
  800      2       5   0.0832  0.0499       0.0257        0.270
  900      1       0   0.0832  0.0499       0.0257        0.270

9.2.3 Kaplan-Meier Plots

Now that we’ve fit a survival curve to the data it’s pretty easy to visualize it with a Kaplan-Meier plot. Create the survival object if you don’t have it yet, and instead of using summary(), use plot() instead.

sfit <- survfit(Surv(time, status)~sex, data=lung)
plot(sfit)

There are lots of ways to modify the plot produced by base R’s plot() function. You can see more options with the help for ?plot.survfit. We’re not going to go into any more detail here, because there’s another package called survminer that provides a function called ggsurvplot() that makes it much easier to produce publication-ready survival plots, and if you’re familiar with ggplot2 syntax it’s pretty easy to modify. So, let’s load the package and try it out.

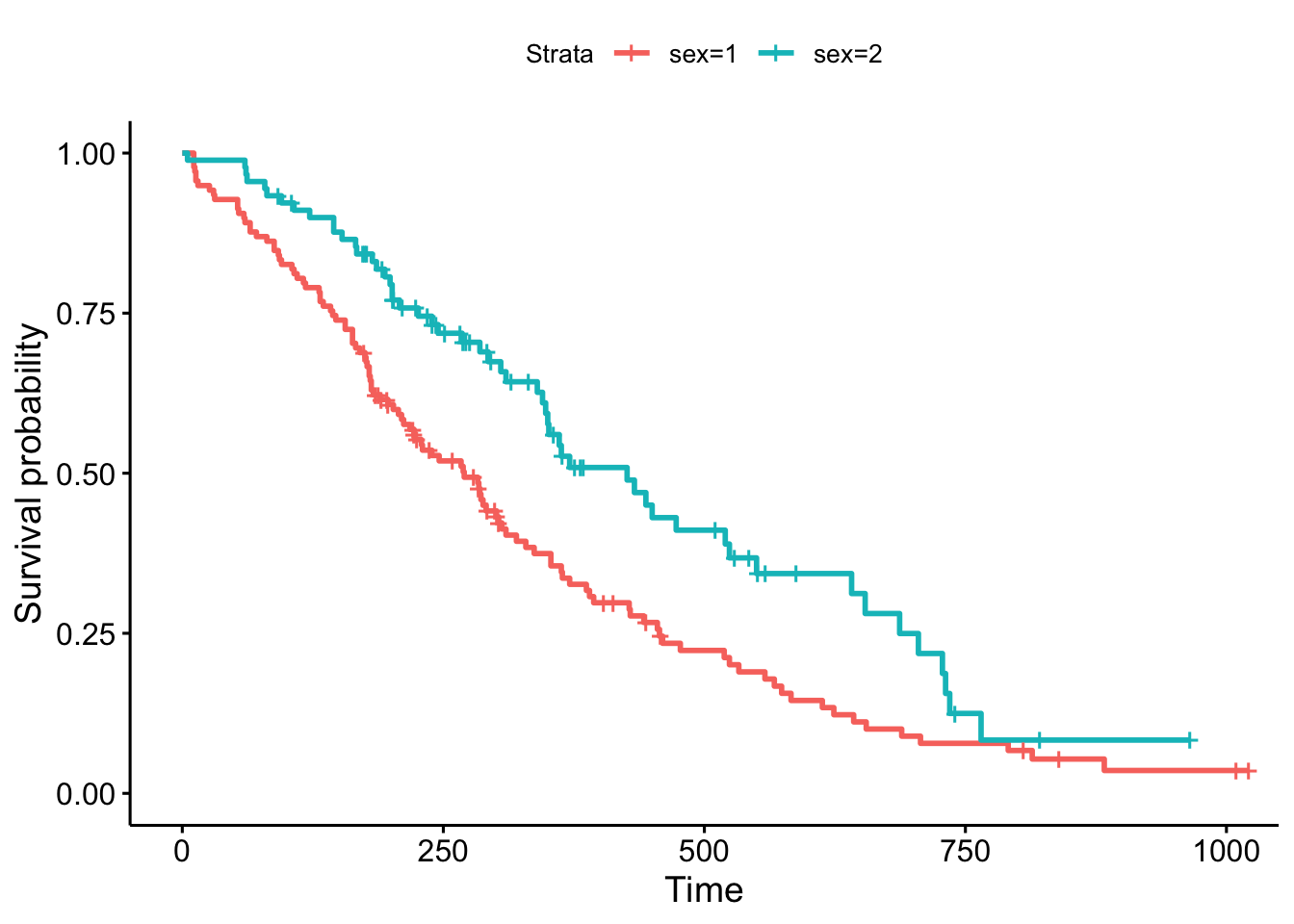
This plot is substantially more informative by default, just because it automatically color codes the different groups, adds axis labels, and creates and automatic legend. But there’s a lot more you can do pretty easily here. Let’s add confidence intervals, show the p-value for the log-rank test, show a risk table below the plot, and change the colors and the group labels.

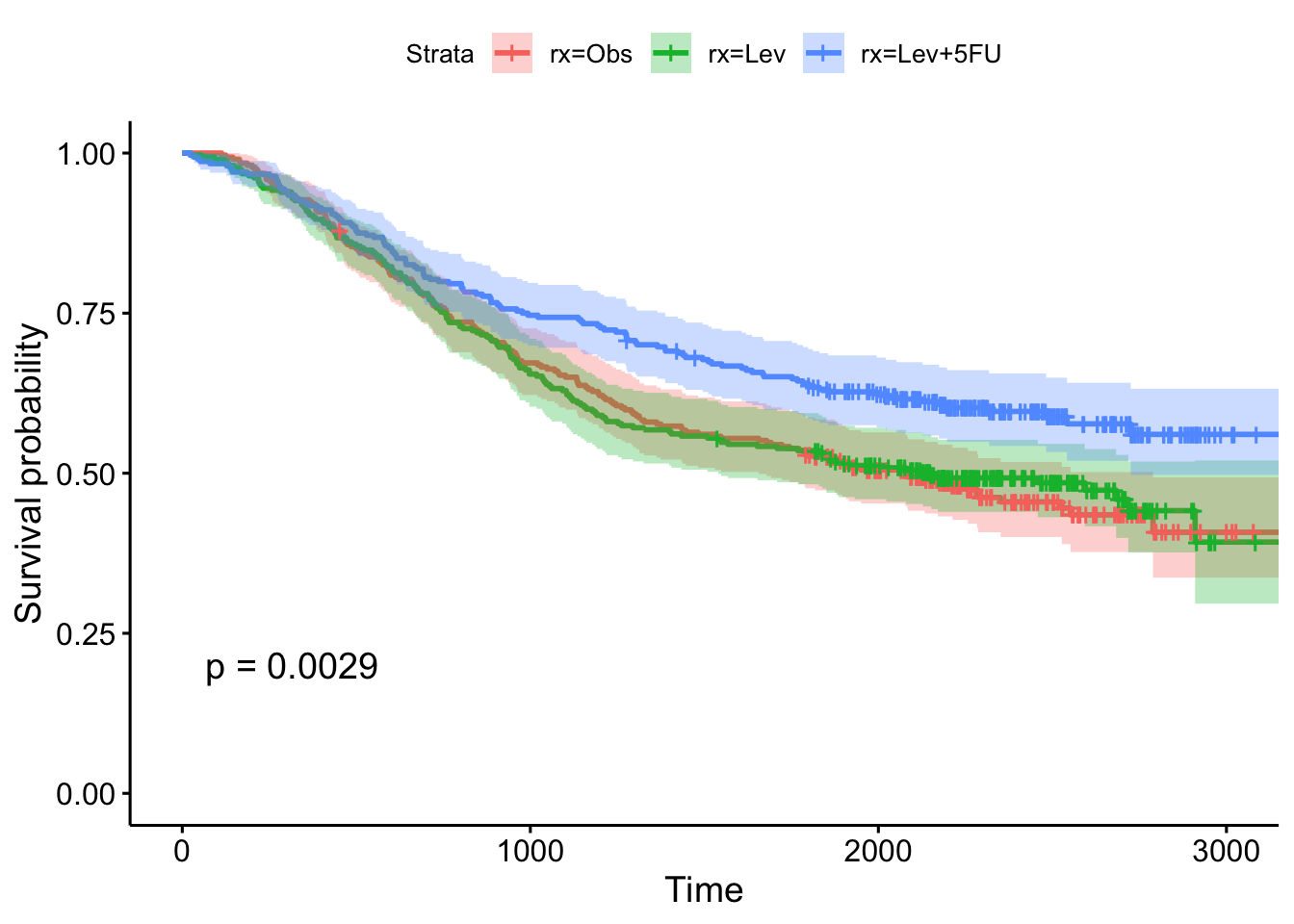
ggsurvplot(sfit, conf.int=TRUE, pval=TRUE, risk.table=TRUE, 
           legend.labs=c("Male", "Female"), legend.title="Sex",  
           palette=c("dodgerblue2", "orchid2"), 
           title="Kaplan-Meier Curve for Lung Cancer Survival", 
           risk.table.height=.15)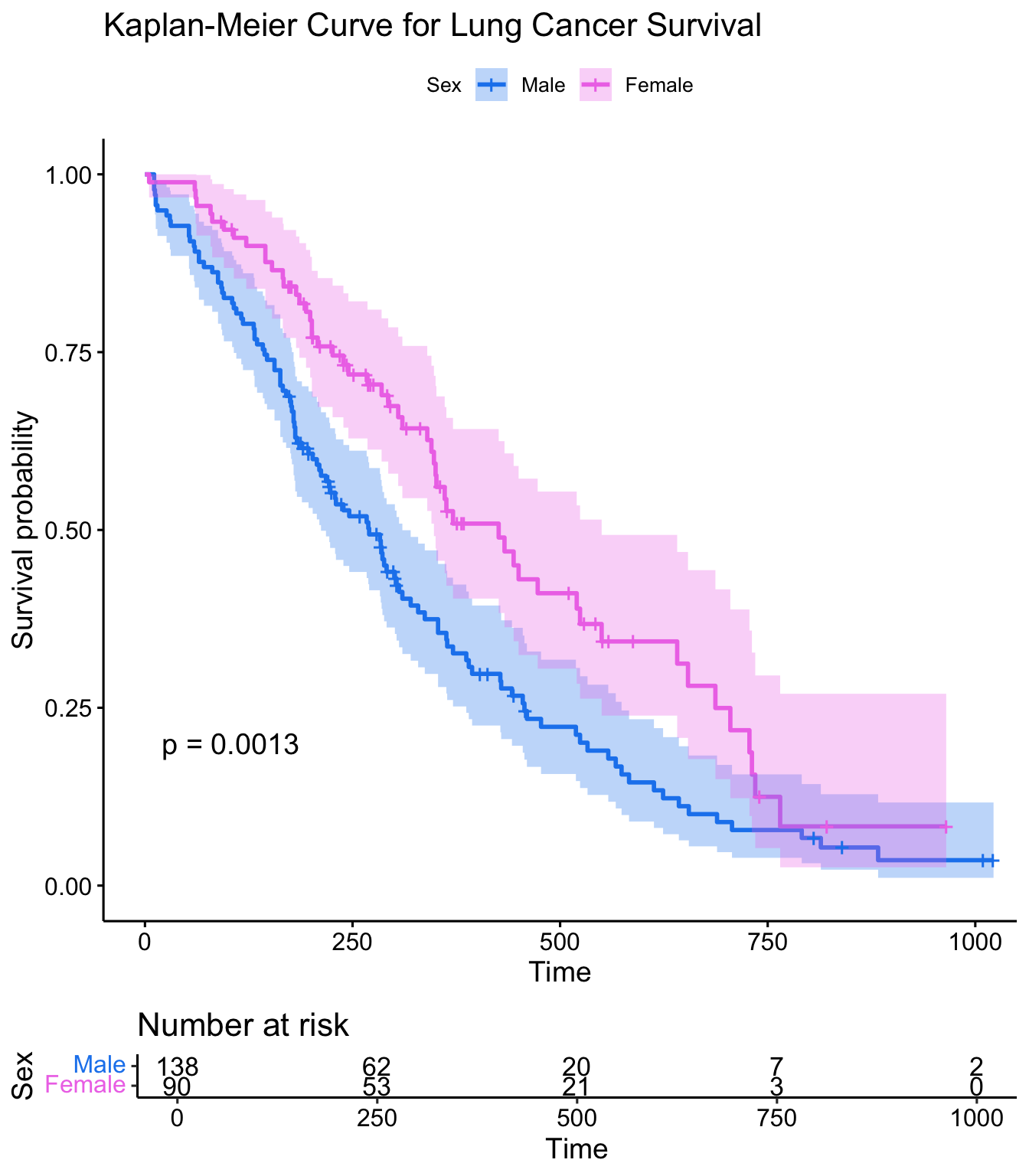

Exercise 1

Take a look at the built in colon dataset. If you type ?colon it’ll ask you if you wanted help on the colon dataset from the survival package, or the colon operator. Click “Chemotherapy for Stage B/C colon cancer”, or be specific with ?survival::colon. This dataset has survival and recurrence information on 929 people from a clinical trial on colon cancer chemotherapy. There are two rows per person, indidicated by the event type (etype) variable – etype==1 indicates that row corresponds to recurrence; etype==2 indicates death.

First, let’s turn the colon data into a tibble, then filter the data to only include the survival data, not the recurrence data. Let’s call this new object colondeath. The filter() function is in the dplyr library, which you can get by running library(dplyr). If you don’t have dplyr you can use the base subset() function instead.

library(dplyr)
colon <- as_tibble(colon)
colondeath <- filter(colon, etype==2)

# Or, using base subset()
# colondeath <- subset(colon, etype==2)

head(colondeath)
# A tibble: 6 × 16
     id study rx        sex   age obstruct perfor adhere nodes status differ
  <dbl> <dbl> <fct>   <dbl> <dbl>    <dbl>  <dbl>  <dbl> <dbl>  <dbl>  <dbl>
1     1     1 Lev+5FU     1    43        0      0      0     5      1      2
2     2     1 Lev+5FU     1    63        0      0      0     1      0      2
3     3     1 Obs         0    71        0      0      1     7      1      2
4     4     1 Lev+5FU     0    66        1      0      0     6      1      2
5     5     1 Obs         1    69        0      0      0    22      1      2
6     6     1 Lev+5FU     0    57        0      0      0     9      1      2
# ℹ 5 more variables: extent <dbl>, surg <dbl>, node4 <dbl>, time <dbl>,
#   etype <dbl>
Exercise 2

Look at the help for ?colon again. How are sex and status coded? How is this different from the lung data?

Exercise 3

Using survfit(Surv(..., ...,)~..., data=colondeath), create a survival curve separately for males versus females. Call the resulting object sfit. Run a summary() on this object, showing time points 0, 500, 1000, 1500, and 2000. Do males or females appear to fair better over this time period?

                sex=0 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    445       0    1.000  0.0000        1.000        1.000
  500    381      64    0.856  0.0166        0.824        0.889
 1000    306      75    0.688  0.0220        0.646        0.732
 1500    265      40    0.598  0.0232        0.554        0.645
 2000    218      22    0.547  0.0236        0.503        0.596

                sex=1 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    484       0    1.000  0.0000        1.000        1.000
  500    418      65    0.866  0.0155        0.836        0.897
 1000    335      83    0.694  0.0210        0.654        0.736
 1500    287      46    0.598  0.0223        0.556        0.644
 2000    238      25    0.545  0.0227        0.503        0.592
Exercise 4

Using the survminer package, plot a Kaplan-Meier curve for this analysis with confidence intervals and showing the p-value. See ?ggsurvplot for help. Is there a significant difference between males and females?

Exercise 5

Create Kaplan-Meier plot stratifying by:

  1. The extent of differentiation (well, moderate, poor), showing the p-value.
  2. Whether or not there was detectable cancer in >=4 lymph nodes, showing the p-value and confidence bands.

9.2.4 Cox Regression

Kaplan-Meier curves are good for visualizing differences in survival between two categorical groups, and the log-rank test you get when you ask for pval=TRUE is useful for asking if there are differences in survival between different groups. But this doesn’t generalize well for assessing the effect of quantitative variables. Just try creating a K-M plot for the nodes variable, which has values that range from 0-33. What a mess! Don’t do this.

ggsurvplot(survfit(Surv(time, status)~nodes, data=colondeath))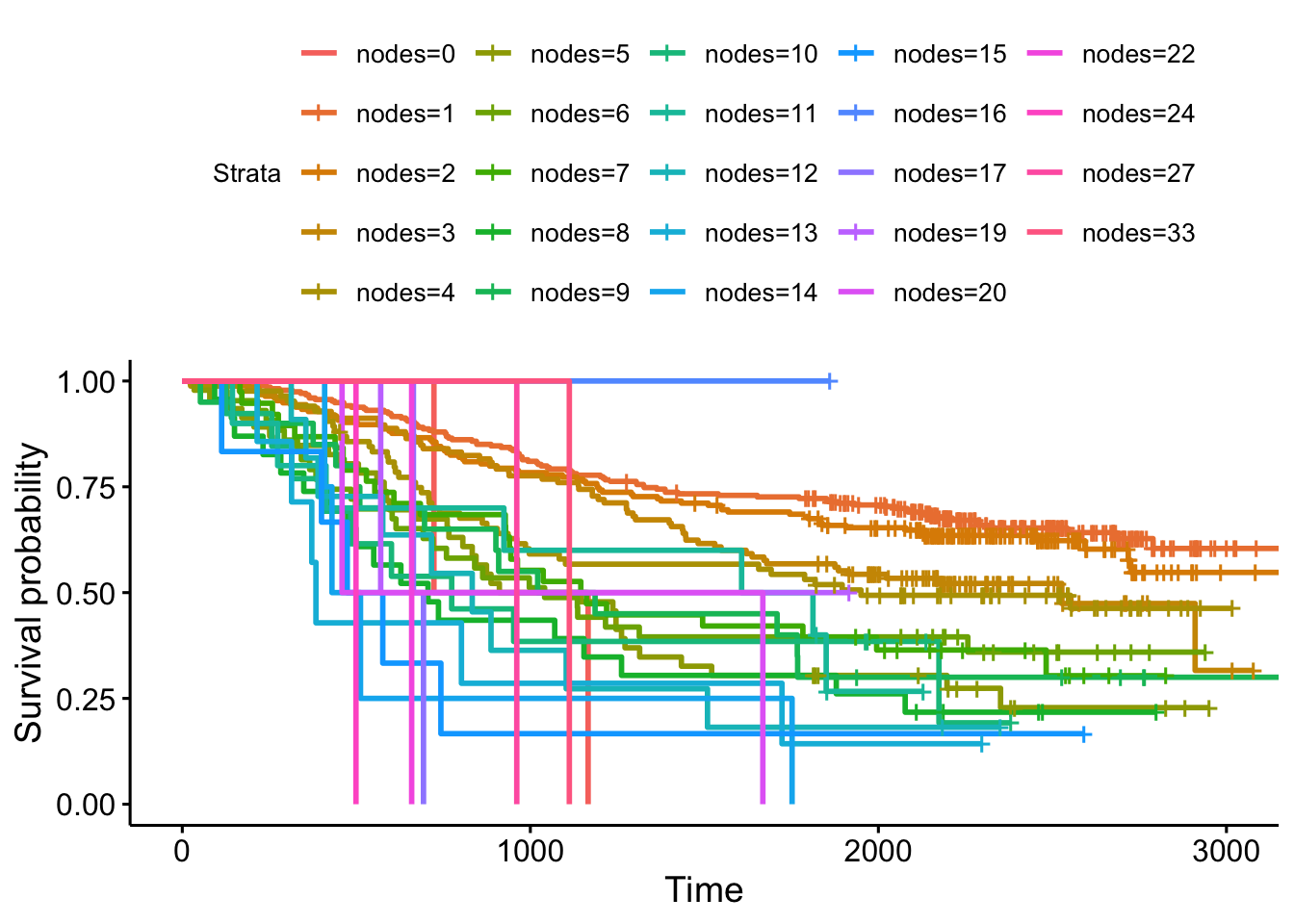

At some point using a categorical grouping for K-M plots breaks down, and further, you might want to assess how multiple variables work together to influence survival. For example, you might want to simultaneously examine the effect of race and socioeconomic status, so as to adjust for factors like income, access to care, etc., before concluding that ethnicity influences some outcome.

Cox PH regression can assess the effect of both categorical and continuous variables, and can model the effect of multiple variables at once. The coxph() function uses the same syntax as lm(), glm(), etc. The response variable you create with Surv() goes on the left hand side of the formula, specified with a ~. Explanatory variables go on the right side.

Let’s go back to the lung cancer data and run a Cox regression on sex.

fit <- coxph(Surv(time, status)~sex, data=lung)
fit
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)

    coef exp(coef) se(coef)  z     p
sex -0.5       0.6      0.2 -3 0.001

Likelihood ratio test=11  on 1 df, p=0.001
n= 228, number of events= 165

The exp(coef) column contains \(e^{\beta_1}\) (see background section above for more info). This is the hazard ratio – the multiplicative effect of that variable on the hazard rate (for each unit increase in that variable). So, for a categorical variable like sex, going from male (baseline) to female results in approximately ~40% reduction in hazard. You could also flip the sign on the coef column, and take exp(0.531), which you can interpret as being male resulting in a 1.7-fold increase in hazard, or that males die ad approximately 1.7x the rate per unit time as females (females die at 0.588x the rate per unit time as males).

Just remember:

  • HR=1: No effect
  • HR>1: Increase in hazard
  • HR<1: Reduction in hazard (protective)

You’ll also notice there’s a p-value on the sex term, and a p-value on the overall model. That 0.00111 p-value is really close to the p=0.00131 p-value we saw on the Kaplan-Meier plot. That’s because the KM plot is showing the log-rank test p-value. You can get this out of the Cox model with a call to summary(fit). You can directly calculate the log-rank test p-value using survdiff().

summary(fit)
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)

  n= 228, number of events= 165 

      coef exp(coef) se(coef)     z Pr(>|z|)
sex -0.531     0.588    0.167 -3.18   0.0015

    exp(coef) exp(-coef) lower .95 upper .95
sex     0.588        1.7     0.424     0.816

Concordance= 0.579  (se = 0.021 )
Likelihood ratio test= 10.6  on 1 df,   p=0.001
Wald test            = 10.1  on 1 df,   p=0.001
Score (logrank) test = 10.3  on 1 df,   p=0.001
survdiff(Surv(time, status)~sex, data=lung)
Call:
survdiff(formula = Surv(time, status) ~ sex, data = lung)

        N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 138      112     91.6      4.55      10.3
sex=2  90       53     73.4      5.68      10.3

 Chisq= 10.3  on 1 degrees of freedom, p= 0.001

Let’s create another model where we analyze all the variables in the dataset! This shows us how all the variables, when considered together, act to influence survival. Some are very strong predictors (sex, ECOG score). Interestingly, the Karnofsky performance score as rated by the physician was marginally significant, while the same score as rated by the patient was not.

fit <- coxph(Surv(time, status)~sex+age+ph.ecog+ph.karno+pat.karno+meal.cal+wt.loss, data=lung)
fit
Call:
coxph(formula = Surv(time, status) ~ sex + age + ph.ecog + ph.karno + 
    pat.karno + meal.cal + wt.loss, data = lung)

            coef exp(coef) se(coef)    z     p
sex       -6e-01     6e-01    2e-01 -2.7 0.006
age        1e-02     1e+00    1e-02  0.9 0.359
ph.ecog    7e-01     2e+00    2e-01  3.3 0.001
ph.karno   2e-02     1e+00    1e-02  2.0 0.046
pat.karno -1e-02     1e+00    8e-03 -1.5 0.123
meal.cal   3e-05     1e+00    3e-04  0.1 0.898
wt.loss   -1e-02     1e+00    8e-03 -1.8 0.065

Likelihood ratio test=28  on 7 df, p=2e-04
n= 168, number of events= 121 
   (60 observations deleted due to missingness)
Exercise 6

Let’s go back to the colon cancer dataset. Remember, you created a colondeath object in the first exercise that only includes survival (etype==2), not recurrence data points. See ?colon for more information about this dataset.

Take a look at levels(colondeath$rx). This tells you that the rx variable is the type of treatment the patient was on, which is either nothing (coded Obs, short for Observation), Levamisole (coded Lev), or Levamisole + 5-fluorouracil (coded Lev+5FU). This is a factor variable coded with these levels, in that order. This means that Obs is treated as the baseline group, and other groups are dummy-coded to represent the respective group.

With k levels of a categorical factor variable, you get k-1 dummy variables created, each 0/1, indicating that the sample is a particular non-reference category. Having value 0 for all dummy variables indicates that the sample is baseline.
rx Lev Lev+5FU
Obs 0 0
Lev 1 0
Lev+5FU 0 1
Exercise 7

Run a Cox proportional hazards regression model against this rx variable. How do you interpret the result? Which treatment seems to be significantly different from the control (Observation)?

           coef exp(coef) se(coef)    z     p
rxLev     -0.03      0.97     0.11 -0.2 0.809
rxLev+5FU -0.37      0.69     0.12 -3.1 0.002

Likelihood ratio test=12  on 2 df, p=0.002
n= 929, number of events= 452
Exercise 8

Show the results using a Kaplan-Meier plot, with confidence intervals and the p-value.

Exercise 9

Fit another Cox regression model accounting for age, sex, and the number of nodes with detectable cancer. Notice the test statistic on the likelihood ratio test becomes much larger, and the overall model becomes more significant. What do you think accounted for this increase in our ability to model survival?

            coef exp(coef) se(coef)    z      p
rxLev     -0.080     0.923    0.112 -0.7    0.5
rxLev+5FU -0.403     0.669    0.121 -3.3  8e-04
age        0.005     1.005    0.004  1.3    0.2
sex       -0.028     0.972    0.096 -0.3    0.8
nodes      0.093     1.097    0.009 10.5 <2e-16

Likelihood ratio test=88  on 5 df, p=<2e-16
n= 911, number of events= 441 
   (18 observations deleted due to missingness)

9.2.5 Categorizing for KM plots

Let’s go back to the lung data and look at a Cox model for age. Looks like age is very slightly significant when modeled as a continuous variable.

coxph(Surv(time, status)~age, data=lung)
Call:
coxph(formula = Surv(time, status) ~ age, data = lung)

     coef exp(coef) se(coef) z    p
age 0.019     1.019    0.009 2 0.04

Likelihood ratio test=4  on 1 df, p=0.04
n= 228, number of events= 165

Now that your regression analysis shows you that age is marginally significant, let’s make a Kaplan-Meier plot. But, as we saw before, we can’t just do this, because we’ll get a separate curve for every unique value of age!

ggsurvplot(survfit(Surv(time, status)~age, data=lung))

One thing you might see here is an attempt to categorize a continuous variable into different groups – tertiles, upper quartile vs lower quartile, a median split, etc – so you can make the KM plot. But, how you make that cut is meaningful! Check out the help for ?cut. cut() takes a continuous variable and some breakpoints and creats a categorical variable from that. Let’s get the average age in the dataset, and plot a histogram showing the distribution of age.

mean(lung$age)
hist(lung$age)
ggplot(lung, aes(age)) + geom_histogram(bins=20)

Now, let’s try creating a categorical variable on lung$age with cut pounts at 0, 62 (the mean), and +Infinity (no upper limit). We could continue adding a labels= option here to label the groupings we create, for instance, as “young” and “old”. Finally, we could assign the result of this to a new object in the lung dataset.

cut(lung$age, breaks=c(0, 62, Inf))
  [1] (62,Inf] (62,Inf] (0,62]   (0,62]   (0,62]   (62,Inf] (62,Inf] (62,Inf]
  [9] (0,62]   (0,62]   (0,62]   (62,Inf] (62,Inf] (0,62]   (0,62]   (62,Inf]
 [17] (62,Inf] (62,Inf] (0,62]   (0,62]   (62,Inf] (0,62]   (0,62]   (0,62]  
 [25] (62,Inf] (62,Inf] (0,62]   (62,Inf] (0,62]   (62,Inf] (62,Inf] (62,Inf]
 [33] (0,62]   (0,62]   (0,62]   (0,62]   (62,Inf] (62,Inf] (62,Inf] (62,Inf]
 [41] (62,Inf] (62,Inf] (0,62]   (0,62]   (62,Inf] (62,Inf] (62,Inf] (62,Inf]
 [49] (62,Inf] (0,62]   (62,Inf] (62,Inf] (62,Inf] (0,62]   (0,62]   (0,62]  
 [57] (62,Inf] (0,62]   (0,62]   (62,Inf] (62,Inf] (0,62]   (62,Inf] (62,Inf]
 [65] (62,Inf] (62,Inf] (62,Inf] (62,Inf] (62,Inf] (62,Inf] (62,Inf] (0,62]  
 [73] (62,Inf] (0,62]   (0,62]   (62,Inf] (0,62]   (0,62]   (62,Inf] (62,Inf]
 [81] (0,62]   (0,62]   (0,62]   (0,62]   (0,62]   (62,Inf] (0,62]   (0,62]  
 [89] (0,62]   (62,Inf] (62,Inf] (62,Inf] (62,Inf] (0,62]   (62,Inf] (62,Inf]
 [97] (62,Inf] (62,Inf] (62,Inf] (62,Inf] (0,62]   (62,Inf] (0,62]   (62,Inf]
[105] (0,62]   (62,Inf] (0,62]   (62,Inf] (0,62]   (62,Inf] (62,Inf] (0,62]  
[113] (62,Inf] (62,Inf] (0,62]   (62,Inf] (0,62]   (62,Inf] (62,Inf] (62,Inf]
[121] (62,Inf] (0,62]   (62,Inf] (62,Inf] (62,Inf] (62,Inf] (0,62]   (62,Inf]
[129] (62,Inf] (0,62]   (0,62]   (0,62]   (0,62]   (0,62]   (62,Inf] (62,Inf]
[137] (0,62]   (0,62]   (0,62]   (0,62]   (62,Inf] (62,Inf] (62,Inf] (62,Inf]
[145] (0,62]   (0,62]   (62,Inf] (0,62]   (62,Inf] (0,62]   (62,Inf] (0,62]  
[153] (0,62]   (0,62]   (0,62]   (62,Inf] (62,Inf] (0,62]   (62,Inf] (0,62]  
[161] (0,62]   (0,62]   (62,Inf] (62,Inf] (62,Inf] (0,62]   (0,62]   (0,62]  
[169] (0,62]   (62,Inf] (0,62]   (0,62]   (0,62]   (0,62]   (0,62]   (0,62]  
[177] (0,62]   (0,62]   (0,62]   (62,Inf] (0,62]   (0,62]   (62,Inf] (62,Inf]
[185] (0,62]   (0,62]   (62,Inf] (0,62]   (62,Inf] (0,62]   (62,Inf] (0,62]  
[193] (0,62]   (62,Inf] (62,Inf] (62,Inf] (62,Inf] (62,Inf] (0,62]   (0,62]  
 [ reached getOption("max.print") -- omitted 28 entries ]
Levels: (0,62] (62,Inf]
cut(lung$age, breaks=c(0, 62, Inf), labels=c("young", "old"))
  [1] old   old   young young young old   old   old   young young young old  
 [13] old   young young old   old   old   young young old   young young young
 [25] old   old   young old   young old   old   old   young young young young
 [37] old   old   old   old   old   old   young young old   old   old   old  
 [49] old   young old   old   old   young young young old   young young old  
 [61] old   young old   old   old   old   old   old   old   old   old   young
 [73] old   young young old   young young old   old   young young young young
 [85] young old   young young young old   old   old   old   young old   old  
 [97] old   old   old   old   young old   young old   young old   young old  
[109] young old   old   young old   old   young old   young old   old   old  
[121] old   young old   old   old   old   young old   old   young young young
[133] young young old   old   young young young young old   old   old   old  
[145] young young old   young old   young old   young young young young old  
[157] old   young old   young young young old   old   old   young young young
[169] young old   young young young young young young young young young old  
[181] young young old   old   young young old   young old   young old   young
[193] young old   old   old   old   old   young young
 [ reached getOption("max.print") -- omitted 28 entries ]
Levels: young old
# the base r way:
lung$agecat <- cut(lung$age, breaks=c(0, 62, Inf), labels=c("young", "old"))

# or the dplyr way:
lung <- lung %>% 
  mutate(agecat=cut(age, breaks=c(0, 62, Inf), labels=c("young", "old")))

head(lung)
# A tibble: 6 × 11
   inst  time status   age   sex ph.ecog ph.karno pat.karno meal.cal wt.loss
  <dbl> <dbl>  <dbl> <dbl> <dbl>   <dbl>    <dbl>     <dbl>    <dbl>   <dbl>
1     3   306      2    74     1       1       90       100     1175      NA
2     3   455      2    68     1       0       90        90     1225      15
3     3  1010      1    56     1       0       90        90       NA      15
4     5   210      2    57     1       1       90        60     1150      11
5     1   883      2    60     1       0      100        90       NA       0
6    12  1022      1    74     1       1       50        80      513       0
# ℹ 1 more variable: agecat <fct>

Now, what happens when we make a KM plot with this new categorization? It looks like there’s some differences in the curves between “old” and “young” patients, with older patients having slightly worse survival odds. But at p=.39, the difference in survival between those younger than 62 and older than 62 are not significant.

ggsurvplot(survfit(Surv(time, status)~agecat, data=lung), pval=TRUE)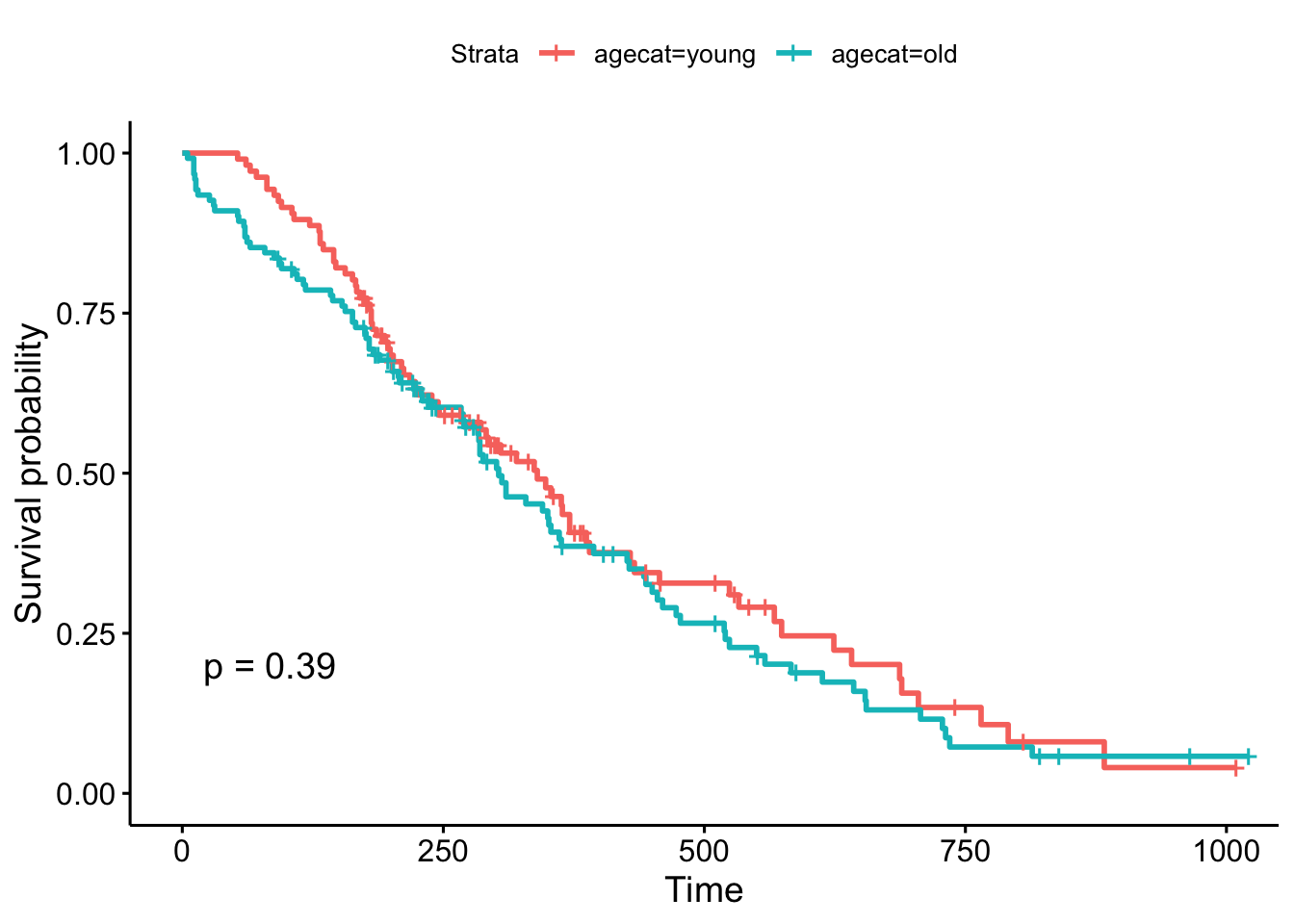

But, what if we chose a different cut point, say, 70 years old, which is roughly the cutoff for the upper quartile of the age distribution (see ?quantile). The result is now marginally significant!

# the base r way:
lung$agecat <- cut(lung$age, breaks=c(0, 70, Inf), labels=c("young", "old"))

# or the dplyr way:
lung <- lung %>% 
  mutate(agecat=cut(age, breaks=c(0, 70, Inf), labels=c("young", "old")))

# plot!
ggsurvplot(survfit(Surv(time, status)~agecat, data=lung), pval=TRUE)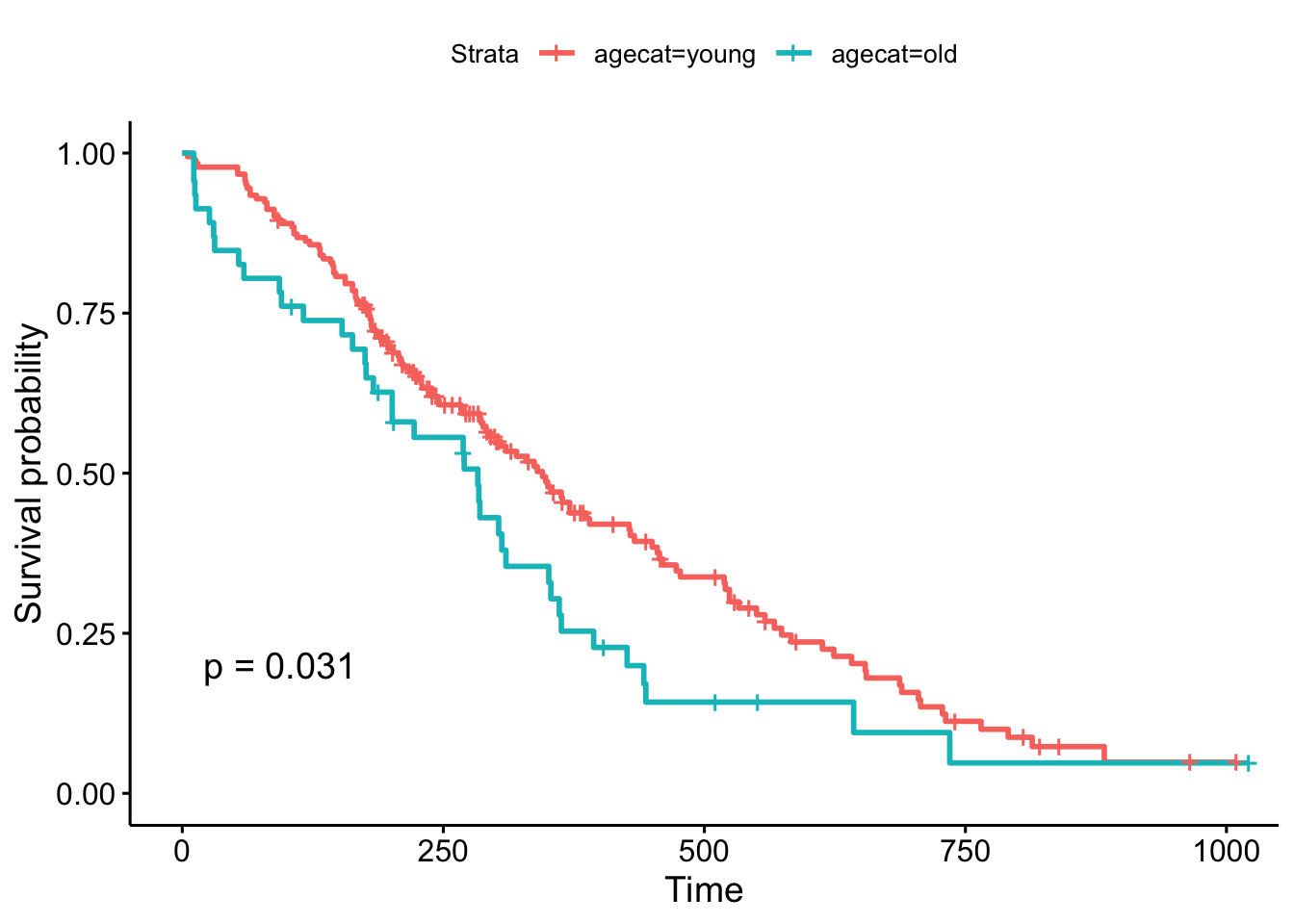

Remember, the Cox regression analyzes the continuous variable over the whole range of its distribution, where the log-rank test on the Kaplan-Meier plot can change depending on how you categorize your continuous variable. They’re answering a similar question in a different way: the regression model is asking, “what is the effect of age on survival?”, while the log-rank test and the KM plot is asking, “are there differences in survival between those less than 70 and those greater than 70 years old?”.

(New in survminer 0.2.4: the survminer package can now determine the optimal cutpoint for one or multiple continuous variables at once, using the surv_cutpoint() and surv_categorize() functions. Refer to this blog post for more information.)

9.3 TCGA

The Cancer Genome Atlas (TCGA) is a collaboration between the National Cancer Institute (NCI) and the National Human Genome Research Institute (NHGRI) that collected lots of clinical and genomic data across 33 cancer types. The entire TCGA dataset is over 2 petabytes worth of gene expression, CNV profiling, SNP genotyping, DNA methylation, miRNA profiling, exome sequencing, and other types of data. You can learn more about TCGA at cancergenome.nih.gov. The data is now housed at the Genomic Data Commons Portal. There are lots of ways to access TCGA data without actually downloading and parsing through the data from GDC. We’ll cover more of these below. But first, let’s look at an R package that provides convenient, direct access to TCGA data.

9.3.1 RTCGA

The RTCGA package (bioconductor.org/packages/RTCGA) and all the associated data packages provide convenient access to clinical and genomic data in TCGA. Each of the data packages is a separate package, and must be installed (once) individually.

# Load the bioconductor installer. 
# Try http:// if https:// doesn't work.
source("https://bioconductor.org/biocLite.R")

# Install the main RTCGA package
biocLite("RTCGA")

# Install the clinical and mRNA gene expression data packages
biocLite("RTCGA.clinical")
biocLite("RTCGA.mRNA")

Let’s load the RTCGA package, and use the infoTCGA() function to get some information about the kind of data available for each cancer type.

9.3.1.1 Survival Analysis with RTCGA Clinical Data

Next, let’s load the RTCGA.clinical package and get a little help about what’s available there.

library(RTCGA.clinical)
?clinical

This tells us all the clinical datasets available for each cancer type. If we just focus on breast cancer, look at how big the data is! There are 1098 rows by 3703 columns in this data alone. Let’s look at some of the variable names. Be careful with View() here – with so many columns, depending on which version of RStudio you have that may or may not have fixed this issue, Viewing a large dataset like this may lock up your RStudio.

dim(BRCA.clinical)
names(BRCA.clinical)
# View(BRCA.clinical)

We’re going to use the survivalTCGA() function from the RTCGA package to pull out survival information from the clinical data. It does this by looking at vital status (dead or alive) and creating a times variable that’s either the days to death or the days followed up before being censored. Look at the help for ?survivalTCGA for more info. You give it a list of clinical datasets to pull from, and a character vector of variables to extract. Let’s look at breast cancer, ovarian cancer, and glioblastoma multiforme. Let’s just extract the cancer type (admin.disease_code).

# Create the clinical data
clin <- survivalTCGA(BRCA.clinical, OV.clinical, GBM.clinical, 
                     extract.cols="admin.disease_code")
# Show the first few lines
head(clin)
           times bcr_patient_barcode patient.vital_status admin.disease_code
379.31.0    3767        TCGA-3C-AAAU                    0               brca
379.31.0.1  3801        TCGA-3C-AALI                    0               brca
379.31.0.2  1228        TCGA-3C-AALJ                    0               brca
379.31.0.3  1217        TCGA-3C-AALK                    0               brca
379.31.0.4   158        TCGA-4H-AAAK                    0               brca
379.31.0.5  1477        TCGA-5L-AAT0                    0               brca
# How many samples of each type?
table(clin$admin.disease_code)

brca  gbm   ov 
1098  595  576 
# Tabulate by outcome
xtabs(~admin.disease_code+patient.vital_status, data=clin) %>% addmargins()
                  patient.vital_status
admin.disease_code    0    1  Sum
              brca  994  104 1098
              gbm   149  446  595
              ov    279  297  576
              Sum  1422  847 2269

Now let’s run a Cox PH model against the disease code. By default it’s going to treat breast cancer as the baseline, because alphabetically it’s first. But you can reorder this if you want with factor().

coxph(Surv(times, patient.vital_status)~admin.disease_code, data=clin)
Call:
coxph(formula = Surv(times, patient.vital_status) ~ admin.disease_code, 
    data = clin)

                         coef exp(coef) se(coef)     z      p
admin.disease_codegbm  2.8875   17.9476   0.1129 25.57 <2e-16
admin.disease_codeov   1.5470    4.6973   0.1153 13.42 <2e-16

Likelihood ratio test=904.3  on 2 df, p=< 2.2e-16
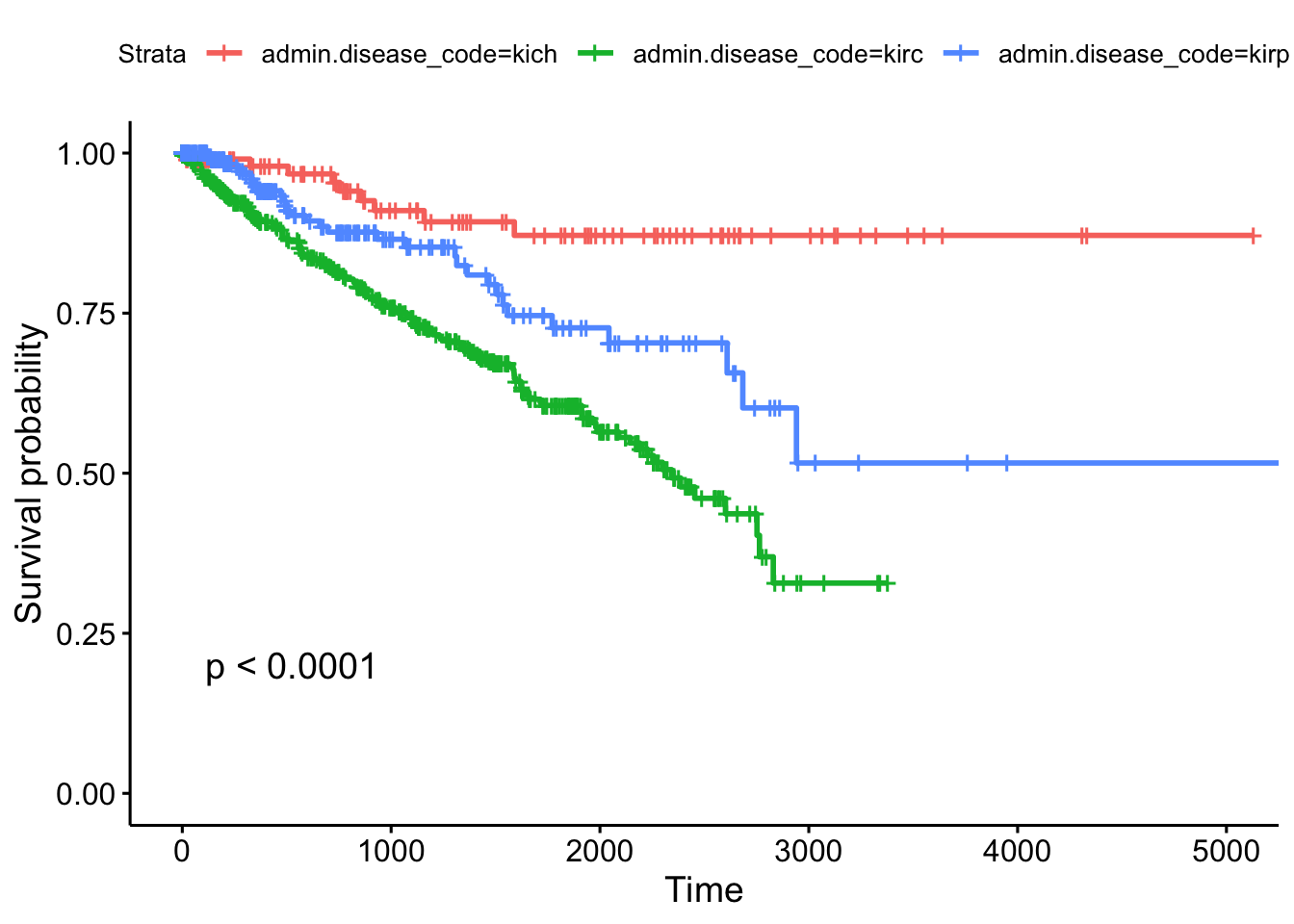
n= 2269, number of events= 847

This tells us that compared to the baseline brca group, GBM patients have a ~18x increase in hazards, and ovarian cancer patients have ~5x worse survival. Let’s create a survival curve, visualize it with a Kaplan-Meier plot, and show a table for the first 5 years survival rates.

sfit <- survfit(Surv(times, patient.vital_status)~admin.disease_code, data=clin)
summary(sfit, times=seq(0,365*5,365))
Call: survfit(formula = Surv(times, patient.vital_status) ~ admin.disease_code, 
    data = clin)

                admin.disease_code=brca 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0   1096       0    1.000 0.00000        1.000        1.000
  365    588      13    0.981 0.00516        0.971        0.992
  730    413      11    0.958 0.00851        0.942        0.975
 1095    304      20    0.905 0.01413        0.878        0.933
 1460    207       9    0.873 0.01719        0.840        0.908
 1825    136      14    0.799 0.02474        0.752        0.849

                admin.disease_code=gbm 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    595       2   0.9966 0.00237       0.9920       1.0000
  365    224     257   0.5110 0.02229       0.4692       0.5567
  730     75     127   0.1998 0.01955       0.1649       0.2420
 1095     39      31   0.1135 0.01617       0.0858       0.1500
 1460     27       9   0.0854 0.01463       0.0610       0.1195
 1825     12       9   0.0534 0.01259       0.0336       0.0847

                admin.disease_code=ov 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    576       0    1.000  0.0000        1.000        1.000
  365    411      59    0.888  0.0139        0.861        0.915
  730    314      55    0.761  0.0198        0.724        0.801
 1095    210      59    0.602  0.0243        0.556        0.651
 1460    133      49    0.451  0.0261        0.402        0.505
 1825     78      39    0.310  0.0260        0.263        0.365
ggsurvplot(sfit, conf.int=TRUE, pval=TRUE)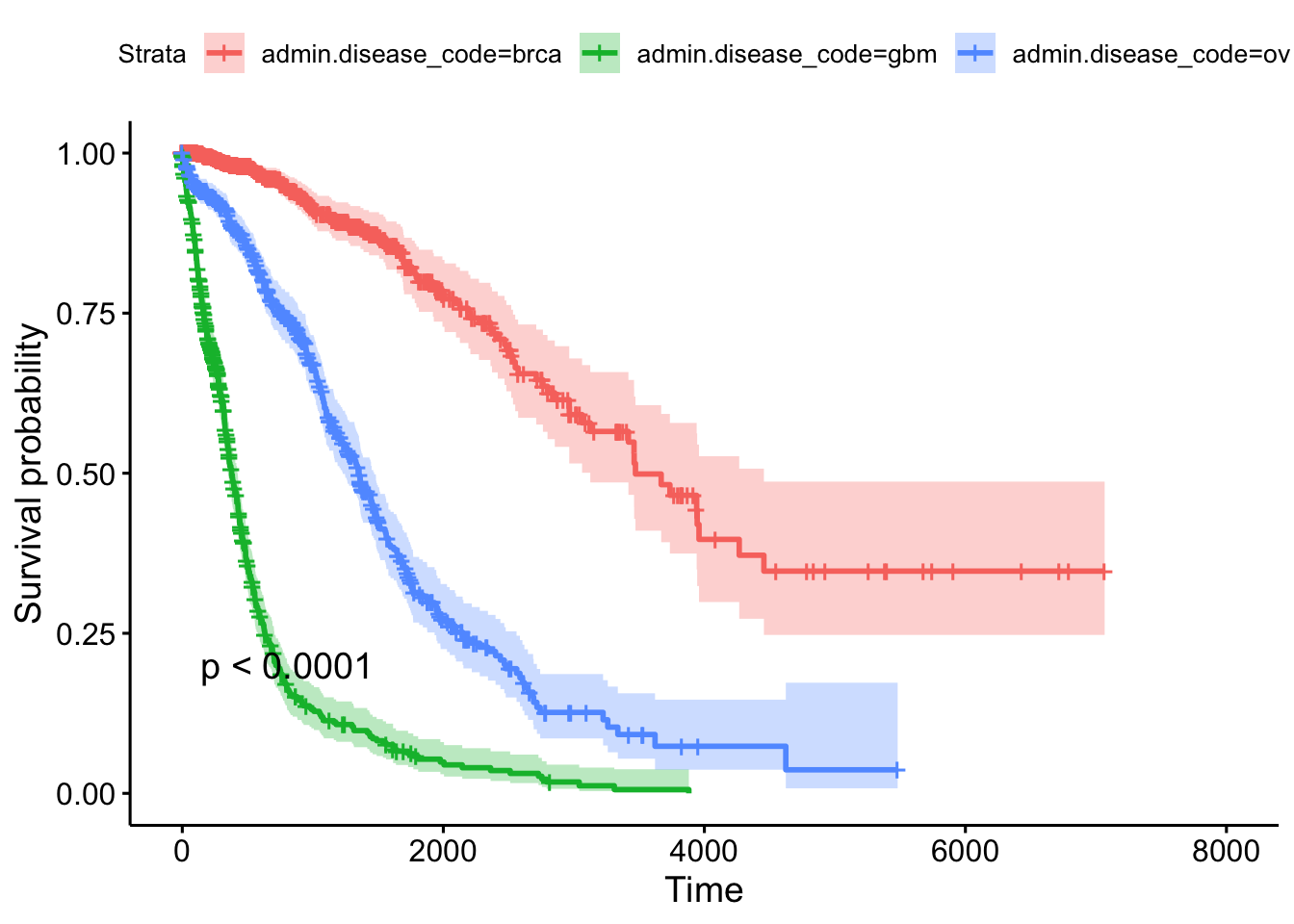

9.3.1.2 Gene Expression Data

Let’s load the gene expression data.

library(RTCGA.mRNA)
?mRNA

Take a look at the size of the BRCA.mRNA dataset, show a few rows and columns.

dim(BRCA.mRNA)
BRCA.mRNA[1:5, 1:5]

Extra credit assignment: See if you can figure out how to join the gene expression data to the clinical data for any particular cancer type.

# Take the mRNA data
BRCA.mRNA %>% 
  # then make it a tibble (nice printing while debugging)
  as_tibble() %>% 
  # then get just a few genes
  select(bcr_patient_barcode, PAX8, GATA3, ESR1) %>% 
  # then trim the barcode (see head(clin), and ?substr)
  mutate(bcr_patient_barcode = substr(bcr_patient_barcode, 1, 12)) %>% 
  # then join back to clinical data
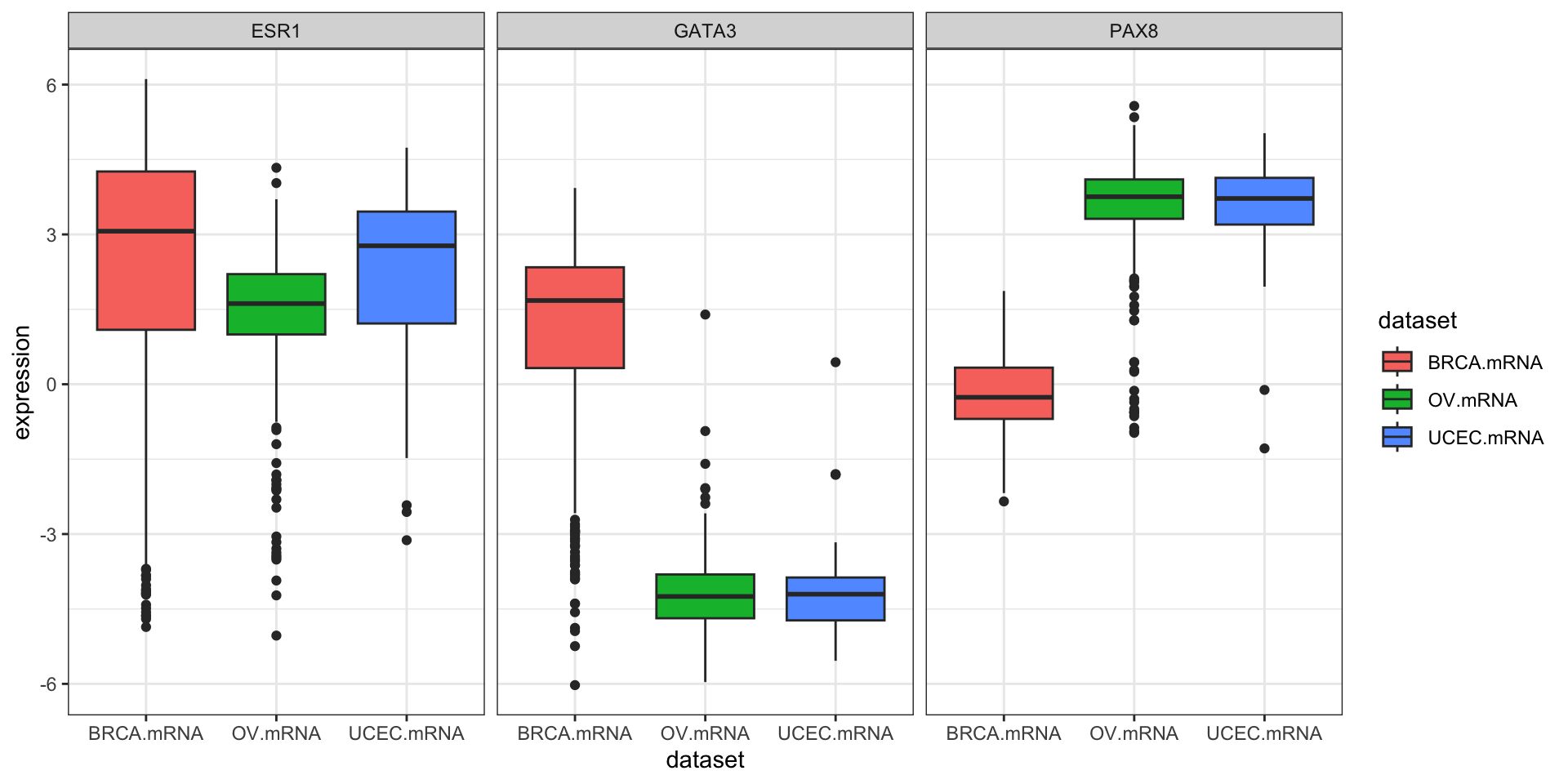
  inner_join(clin, by="bcr_patient_barcode")

Similar to how survivalTCGA() was a nice helper function to pull out survival information from multiple different clinical datasets, expressionsTCGA() can pull out specific gene expression measurements across different cancer types. See the help for ?expressionsTCGA. Let’s pull out data for PAX8, GATA-3, and the estrogen receptor genes from breast, ovarian, and endometrial cancer, and plot the expression of each with a box plot.

library(ggplot2)
expr <- expressionsTCGA(BRCA.mRNA, OV.mRNA, UCEC.mRNA,
                        extract.cols = c("PAX8", "GATA3", "ESR1"))
head(expr)
# A tibble: 6 × 5
  bcr_patient_barcode          dataset     PAX8 GATA3   ESR1
  <chr>                        <chr>      <dbl> <dbl>  <dbl>
1 TCGA-A1-A0SD-01A-11R-A115-07 BRCA.mRNA -0.542  2.87  3.08 
2 TCGA-A1-A0SE-01A-11R-A084-07 BRCA.mRNA -0.595  2.17  2.39 
3 TCGA-A1-A0SH-01A-11R-A084-07 BRCA.mRNA  0.500  1.32  0.791
4 TCGA-A1-A0SJ-01A-11R-A084-07 BRCA.mRNA -0.588  1.84  2.50 
5 TCGA-A1-A0SK-01A-12R-A084-07 BRCA.mRNA -0.965 -6.03 -4.86 
6 TCGA-A1-A0SM-01A-11R-A084-07 BRCA.mRNA  0.573  1.80  2.80 
table(expr$dataset)

BRCA.mRNA   OV.mRNA UCEC.mRNA 
      590       561        54 
ggplot(expr, aes(dataset, PAX8, fill=dataset)) + geom_boxplot()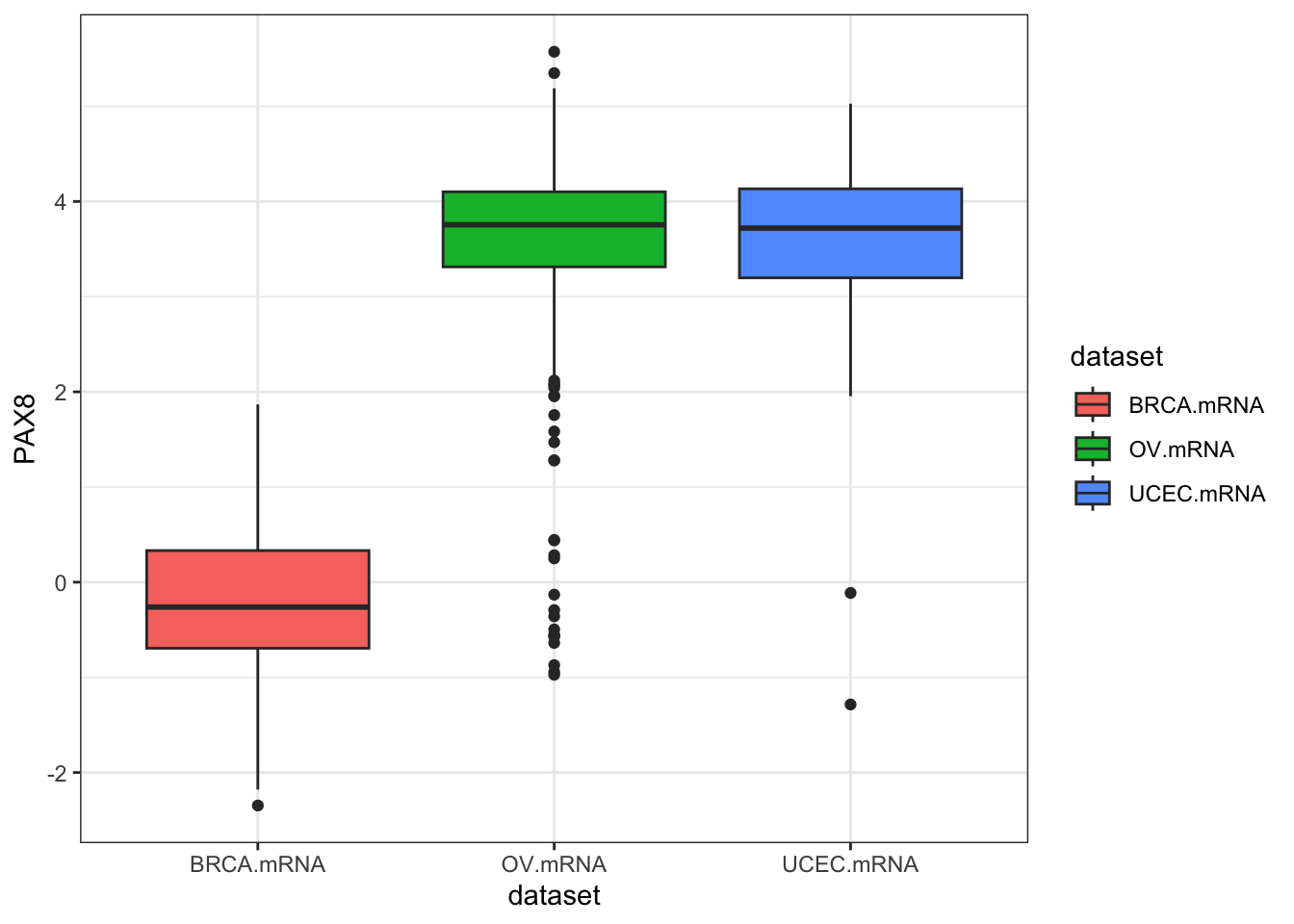

ggplot(expr, aes(dataset, GATA3, fill=dataset)) + geom_boxplot()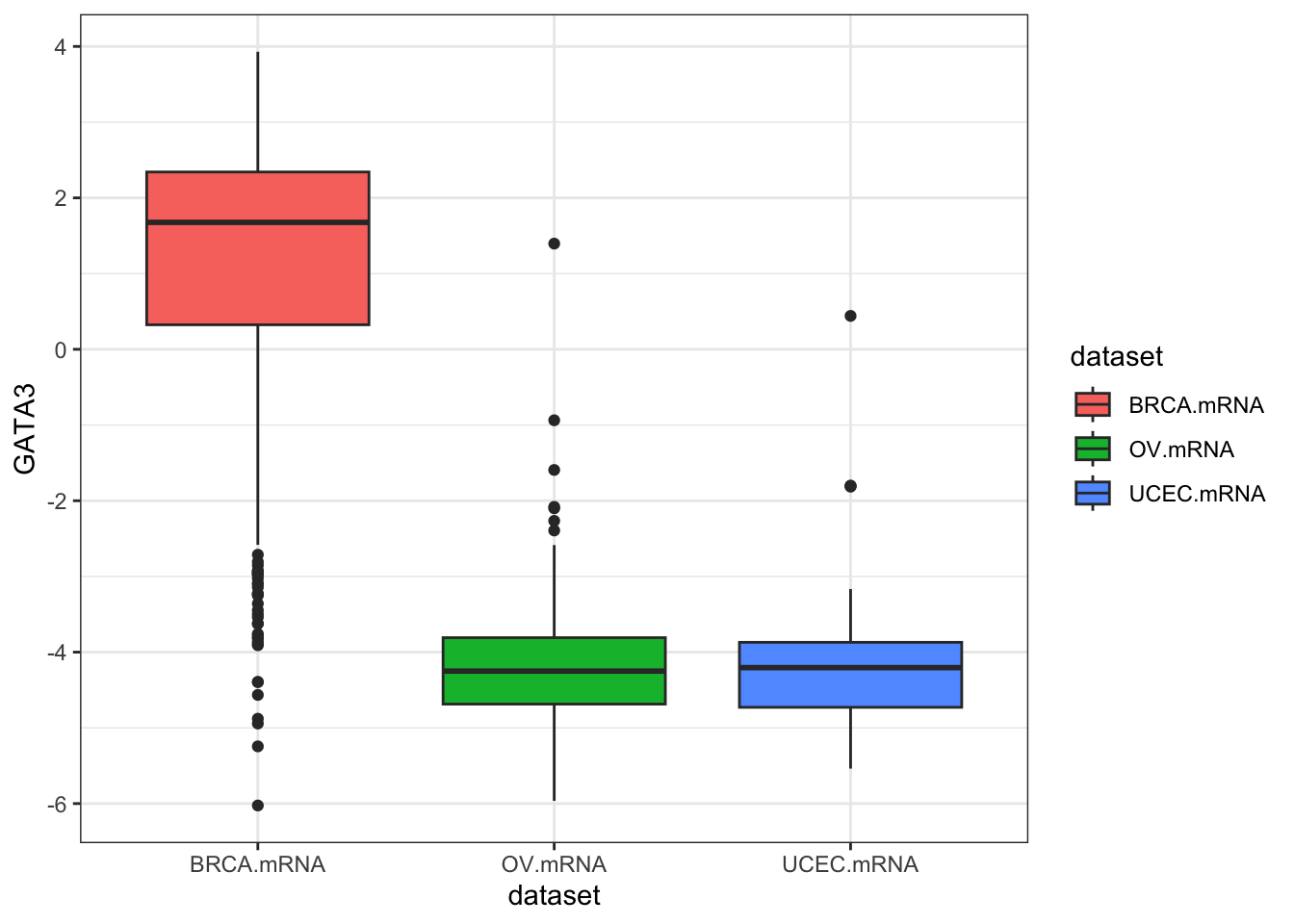

ggplot(expr, aes(dataset, ESR1, fill=dataset)) + geom_boxplot()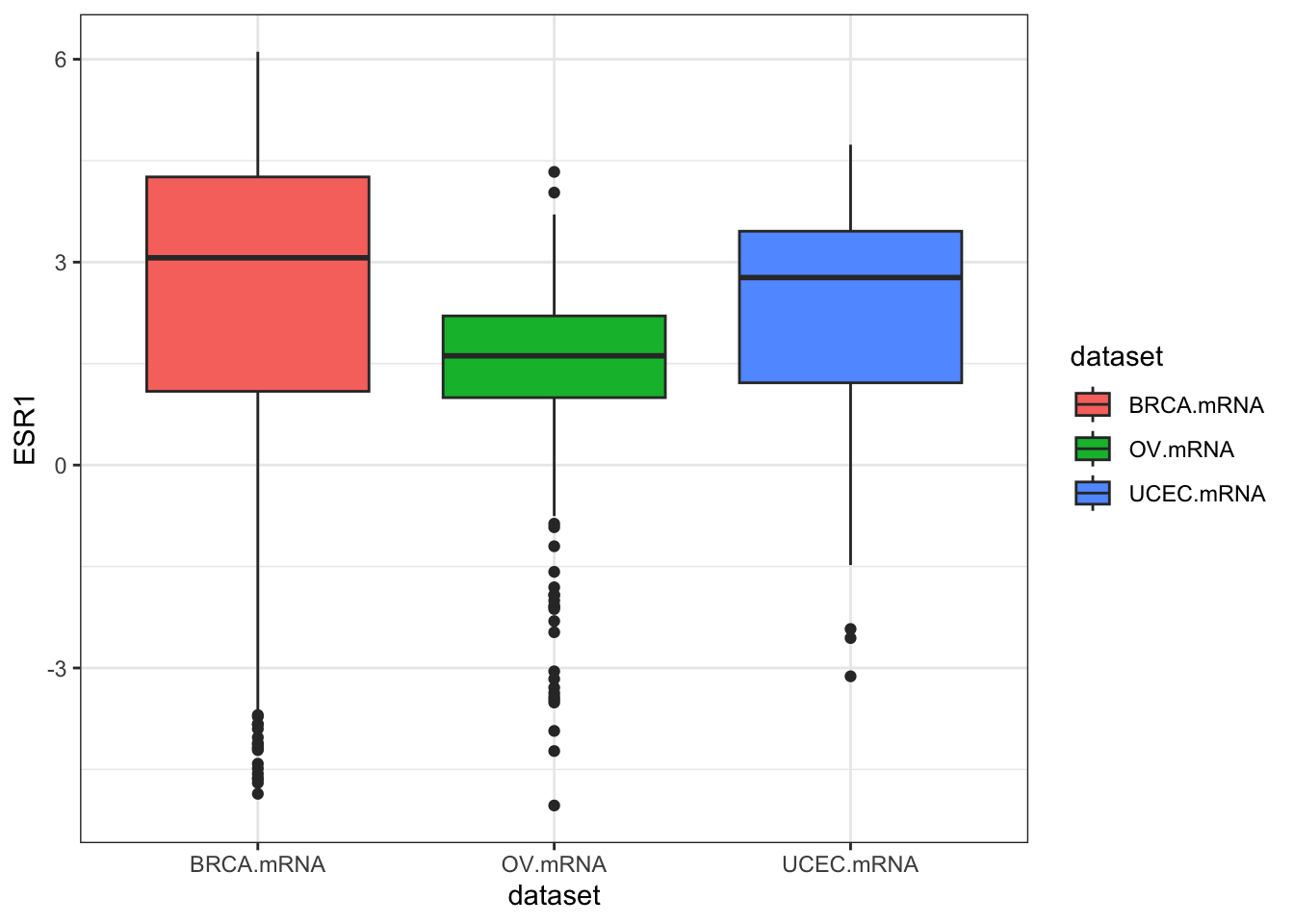

ggplot(expr, aes(dataset, ESR1, fill=dataset)) + geom_violin()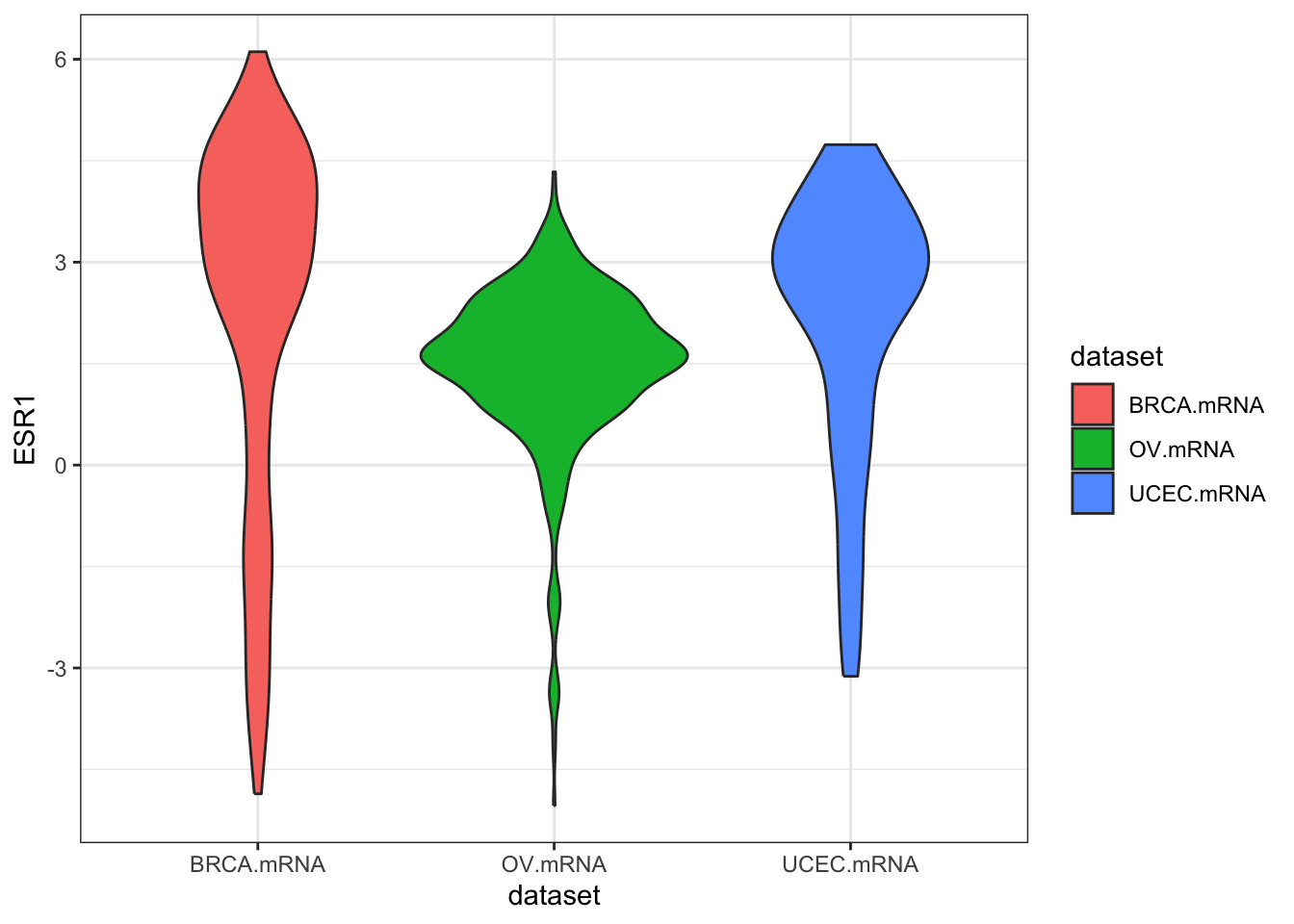

We could also use tidyr to do this all in one go.

library(tidyr)
expr %>% 
  as_tibble() %>% 
  gather(gene, expression, PAX8, GATA3, ESR1) %>% 
  ggplot(aes(dataset, expression, fill=dataset)) + 
    geom_boxplot() + 
    facet_wrap(~gene)

Exercise 10

The “KIPAN” cohort (in KIPAN.clinical) is the pan-kidney cohort, consisting of KICH (chromaphobe renal cell carcinoma), KIRC (renal clear cell carcinoma), and KIPR (papillary cell carcinoma). The KIPAN.clinical has KICH.clinical, KIRC.clinical, and KIPR.clinical all combined.

Using survivalTCGA(), create a new object called clinkid using the KIPAN.clinical cohort. For the columns to extract, get both the disease code and the patient’s gender (extract.cols=c("admin.disease_code", "patient.gender")). The first few rows will look like this.

           times bcr_patient_barcode patient.vital_status admin.disease_code
226.62.0    1158        TCGA-KL-8323                    1               kich
226.62.0.1  4311        TCGA-KL-8324                    0               kich
226.62.0.2   725        TCGA-KL-8325                    1               kich
226.62.0.3  3322        TCGA-KL-8326                    0               kich
226.62.0.4  3553        TCGA-KL-8327                    0               kich
226.62.0.5  3127        TCGA-KL-8328                    0               kich
           patient.gender
226.62.0           female
226.62.0.1         female
226.62.0.2         female
226.62.0.3           male
226.62.0.4         female
226.62.0.5           male
Exercise 11

The xtabs() command will produce tables of counts for categorical variables. Here’s an example for how to use xtabs() for the built-in colon cancer dataset, which will tell you the number of samples split by sex and by treatment.

xtabs(~rx+sex, data=colon)
         sex
rx          0   1
  Obs     298 332
  Lev     266 354
  Lev+5FU 326 282

Use the same command to examine how many samples you have for each kidney sample type, separately by sex.

                  patient.gender
admin.disease_code female male
              kich     51   61
              kirc    191  346
              kirp     76  212
Exercise 12

Run a Cox PH regression on the cancer type and gender. What’s the effect of gender? Is it significant? How does survival differ by each type? Which has the worst prognosis?

                           coef exp(coef) se(coef)      z        p
admin.disease_codekirc  1.59288   4.91791  0.34500  4.617 3.89e-06
admin.disease_codekirp  0.99620   2.70798  0.38069  2.617  0.00887
patient.gendermale     -0.06282   0.93911  0.14841 -0.423  0.67207

Likelihood ratio test=39.43  on 3 df, p=1.404e-08
n= 937, number of events= 203
Exercise 13

Create survival curves for each different subtype. a. Produce a Kaplan-Meier plot. b. Show survival tables each year for the first 5 years.

Call: survfit(formula = Surv(times, patient.vital_status) ~ admin.disease_code, 
    data = clinkid)

                admin.disease_code=kich 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    111       0    1.000  0.0000        1.000        1.000
  365     86       2    0.980  0.0144        0.952        1.000
  730     72       2    0.954  0.0226        0.911        0.999
 1095     54       3    0.910  0.0329        0.848        0.977
 1460     44       1    0.893  0.0366        0.824        0.967
 1825     38       1    0.871  0.0415        0.794        0.957

                admin.disease_code=kirc 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    536       0    1.000  0.0000        1.000        1.000
  365    385      49    0.895  0.0142        0.868        0.924
  730    313      32    0.816  0.0186        0.781        0.853
 1095    250      26    0.744  0.0217        0.703        0.788
 1460    181      20    0.678  0.0243        0.633        0.728
 1825    112      16    0.606  0.0277        0.554        0.663

                admin.disease_code=kirp 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    0    288       0    1.000  0.0000        1.000        1.000
  365    145      10    0.941  0.0182        0.906        0.977
  730    100       8    0.877  0.0278        0.824        0.933
 1095     67       2    0.853  0.0316        0.793        0.917
 1460     54       3    0.810  0.0388        0.737        0.889
 1825     36       5    0.727  0.0495        0.636        0.831

9.3.2 Other TCGA Resources

RTCGA isn’t the only resource providing easy access to TCGA data. In fact, it isn’t even the only R/Bioconductor package. Take a look at some of the other resources shown below.

  • TCGAbiolinks: another R package that allows direct query and analysis from the NCI GDC.
  • cBioPortal: cbioportal.org
    • Nice graphical user interface
    • Quick/easy summary info on patients, demographics, mutations, copy number alterations, etc.
    • Query individual genes, find coexpressed genes
    • Survival analysis against different subtypes, expression, CNAs, etc.
  • OncoLnc: oncolnc.org
    • Focus on survival analysis and RNA-seq data.
    • Simple query interface across all cancers for any mRNA, miRNA, or lncRNA gene (try SERPINA1)
    • Precomputed Cox PH regression for every gene, for every cancer
    • Kaplan-Meier plots produced on demand
  • TANRIC: focus on noncoding RNA
  • MEXPRESS: focus on methylation and gene expression

  1. In the medical world, we typically think of survival analysis literally – tracking time until death. But, it’s more general than that – survival analysis models time until an event occurs (any event). This might be death of a biological organism. But it could also be the time until a hardware failure in a mechanical system, time until recovery, time someone remains unemployed after losing a job, time until a ripe tomato is eaten by a grazing deer, time until someone falls asleep in a workshop, etc. Survival analysis also goes by reliability theory in engineering, duration analysis in economics, and event history analysis in sociology.↩︎

  2. This describes the most common type of censoring – right censoring. Left censoring less commonly occurs when the “start” is unknown, such as when an initial diagnosis or exposure time is unknown.↩︎

  3. And, following the definitions above, assumes that the cumulative hazard ratio between two groups remains constant over time.↩︎

  4. And there’s a chi-square-like statistical test for these differences called the log-rank test that compare the survival functions categorical groups.↩︎

  5. See the multiple regression section of the essential statistics section (Chapter 8).↩︎

  6. Cox regression and the logrank test from survdiff are going to give you similar results most of the time. The log-rank test is asking if survival curves differ significantly between two groups. Cox regression is asking which of many categorical or continuous variables significantly affect survival.↩︎

  7. Surv() can also take start and stop times, to account for left censoring. See the help for ?Surv.↩︎

  8. Loprinzi et al. Prospective evaluation of prognostic variables from patient-completed questionnaires. North Central Cancer Treatment Group. Journal of Clinical Oncology. 12(3):601-7, 1994.↩︎

  9. Where “dead” really refers to the occurance of the event (any event), not necessarily death.↩︎